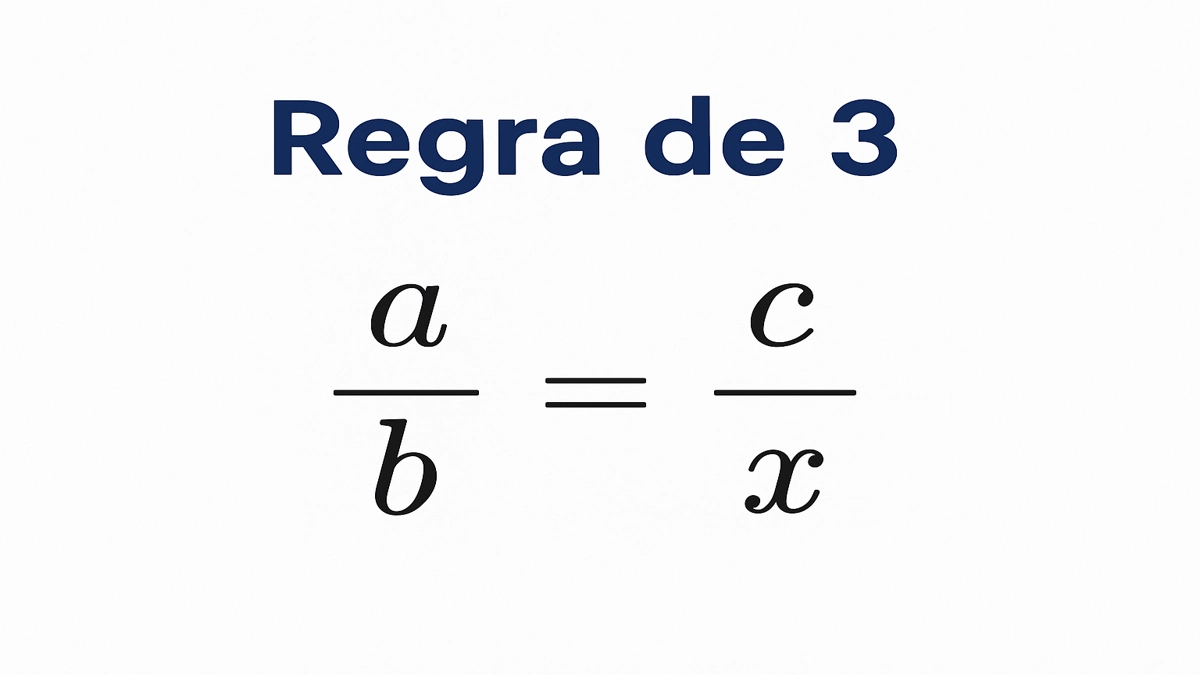Aprender a regra de 3 é essencial para resolver situações que envolvem proporções, desde compras no mercado até cálculos financeiros. Com ela, você encontra valores desconhecidos de forma rápida e confiável.
Essa técnica organiza o raciocínio e evita erros comuns, pois permite comparar grandezas e identificar se a relação é direta ou inversa. O segredo está em montar a proporção corretamente e aplicar o cálculo.
Neste guia, você verá o conceito, exemplos práticos, a aplicação na forma simples e composta, erros para evitar e um plano de estudo. Ao final, terá segurança para usar a regra de 3 em qualquer situação.
Como fazer regra de 3 simples
Primeiro, descubra se a relação é direta ou inversa. Depois, monte a tabela com valores conhecidos e o valor a encontrar. Mantenha as unidades iguais para evitar erros.
- Identifique as grandezas e padronize as unidades.
- Classifique a relação como direta ou inversa.
- Monte a proporção: (frac{text{valor conhecido}}{text{valor correspondente}} = frac{text{valor procurado}}{x}).
- Cruze os termos e isole o valor desejado.
- Confira se o resultado faz sentido no contexto.
Exemplo direto: 5 camisetas custam R$150,00. Quanto custam 8? Montamos: (frac{5}{150} = frac{8}{x}). Cruzando: (5x = 1200 Rightarrow x = 240).
Exemplo inverso: 4 pintores fazem o serviço em 6h. Quantas horas 3 pintores precisarão? Relação inversa, portanto invertemos a razão antes de cruzar os valores. O cálculo mostra que serão necessárias 8 horas.
Exemplo de regra de 3 composta
Se 4 pintores pintam 2 casas em 6 horas, quantos pintores são necessários para pintar 3 casas em 8 horas?
- Mais casas exigem mais pintores (relação direta).
- Mais tempo disponível exige menos pintores (relação inversa).
Montagem: (frac{4}{x} = frac{2}{3} times frac{8}{6}). Para a relação com tempo, invertemos (frac{6}{8}) para (frac{8}{6}) por ser inversa.
Isolando o x: (frac{4}{x} = frac{16}{18} Rightarrow 16x = 72 Rightarrow x = 4,5). O resultado é 4,5 pintores, ou seja, 5 pintores arredondando para o número inteiro mais próximo.
Erros comuns e como corrigir
- Usar unidades diferentes sem padronizar.
- Trocar a ordem dos valores na comparação.
- Esquecer de ajustar quando a relação for inversa.
- Arredondar antes de concluir o cálculo.
Aplicação em porcentagem
Um produto custa R$250,00 e tem 12% de desconto. Montamos: (frac{100}{250} = frac{12}{x}). Cruzando: (100x = 3000 Rightarrow x = 30).
O desconto é de R$30,00 e o novo preço fica R$220,00. Essa mesma lógica pode ser aplicada para calcular juros, comissões e reajustes de preços.
Plano de estudo
- Resolver 5 exercícios por dia (2 diretos, 2 inversos, 1 composto).
- Sempre escrever as unidades junto aos valores.
- Alterar dados de um mesmo problema para identificar padrões.
- Verificar se o resultado está dentro do esperado antes de finalizar.
Para treinar cálculos mais avançados, você pode usar uma calculadora científica online e simular diferentes cenários.
Conclusão
A regra de 3 é um método simples e versátil. Serve para resolver problemas do dia a dia e também cálculos mais detalhados, desde que você monte corretamente a proporção e entenda a relação entre as grandezas.
Com prática constante, é possível ganhar velocidade, confiança e precisão, aplicando essa técnica em qualquer contexto com segurança.